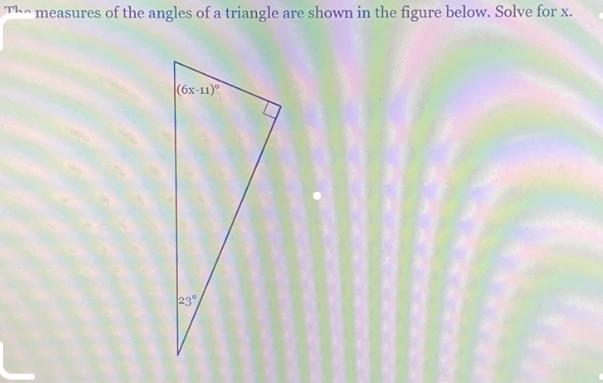
The measures of the angles of a triangle are shown in the figure below. Solve for x.
(6x-11)⁰
23°

PLS HURRY PLS !! :(

The fourth equation which is tan x = [tex]\frac{7000}{5000}[/tex] is the correct way to calculate x. This has been obtained by using trigonometry.

What is trigonometry?

Trigonometry is the study of right-angled triangles, which includes the sides, angles, and connections of each triangle.

We are given that the airplane is 5,000 ft above ground and has to land on a runway that is 7,000 ft away with an angle x.

Since, we are not given the hypotenuse so, we will use tan θ.

We know that in trigonometry, tan θ is calculated as the ratio of the opposite side to the adjacent side.

So,

tan x = [tex]\frac{7000}{5000}[/tex]

Hence, the fourth equation is the correct answer.

Learn more about trigonometry from the given link

https://brainly.com/question/13729598

#SPJ1

The complete question has been attached below

Answer:

y = 8x-19

Step-by-step explanation:

The first step is to find the slope.

m= ( y2-y1)/(x2-x1)

  = ( 13-5)/(4-3)

   = 8/1

  = 8

Then we can use the slope intercept formula.

y = mx+b

y = 8x+b

Substitute a point to find the intercept.

5 = 8*3+b

5 = 24+b

-19 = b

The formula is

y = 8x-19

Answer:

y = 8x - 19

Step-by-step explanation:

the equation of a line in slope- intercept form is

y = mx + c ( m is the slope and c the y- intercept )

calculate m using the slope formula

m = [tex]\frac{y_{2}-y_{1} }{x_{2}-x_{1} }[/tex]

with (x₁, y₁ ) = (3, 5 ) and (x₂, y₂ ) = (4, 13 )

m = [tex]\frac{13-5}{4-3}[/tex] = [tex]\frac{8}{1}[/tex] = 8 , then

y = 8x + c ← is the partial equation

to find c substitute either of the 2 points into the partial equation

using (3, 5 )

5 = 8(3) + c = 24 + c ( subtract 24 from both sides )

- 19 = c

y = 8x - 19 ← equation of line

Answer:

61.38

Step-by-step explanation:

9.30×6.6=61.38

btw u could've used a calculator

Answer:

C

Step-by-step explanation:

The red graph is obtained by shifting the graph of f(x) = 4 - x² upwards by some amount. We can see that the highest point on the red graph occurs at x = 0, where the value is 4.

To shift the graph of f(x) upwards by 3 units, we can add 3 to the entire function:

f(x) + 3 = 4 - x² + 3

= 7 - x²

So the equation of the red graph is:

g(x) = 7 - x²

Therefore, the correct answer is option C: g(x) = 7 - x².

There are 1960 different ways to distribute 8 identical pieces of candy to the five children, where the twins get an equal amount of candy.

First, distribute the candy to the twins.

Split the 8 pieces of candy into two equal parts for the twins using combinations:

C(8, 4)

This means selecting 4 pieces of candy from the 8 identical pieces for one twin, and the remaining 4 pieces will automatically go to the other twin.

C(8, 4) is calculated as:

[tex]^8C_4 = \dfrac{8!}{4!(8-4)!}[/tex]

     = 8! / (4! * 4!)

     = (8 * 7 * 6 * 5) / (4 * 3 * 2 * 1)

     = 70

Now, you have distributed 4 pieces of candy to each of the twins. Y

In this case, you have 6 pieces of candy to distribute among 3 children, and you can use two dividers (bars) to separate the candy for each child.

This can be represented as:

OO|OO|OO

The two bars split the 6 pieces of candy into three sections for the three children.

So, you have C(6 + 2, 2) ways to distribute the remaining candy:

[tex]^{6+2}C_2 = \dfrac{8!}{2!(8-2)!}[/tex]

         = 8! / (2!(8 - 2)!)

         = 8! / (2! * 6!)

         = (8 * 7) / (2 * 1)

         = 28

Now, the total number of ways to distribute the candy

Total ways = C(8, 4) * C(8, 2) = 70 * 28 = 1960

So, there are 1960 different ways to distribute.

Learn more about Combination here:

https://brainly.com/question/29595163

#SPJ12

There is only one possible triangle that can be drawn with one angle measuring 30 deg and another measuring 110°. This is because all triangles have a sum of 180° for the three angles.

Triangle is a three-sided polygon with three straight sides that intersect at three vertices. It is one of the basic shapes in geometry, and is considered to be a building block of other shapes. Triangles can be classified according to their sides, angles, and area. The most common types of triangles are equilateral, isosceles, and scalene triangles, which are classified according to the length of their sides. Triangles can also be classified according to their angles, as acute, right, and obtuse triangles, which are classified according to the size of their angles. Additionally, the area of a triangle is determined by its base, height, and side lengths.

Therefore if one angle is 30° and the other is 110°, the third angle must be 40° for the triangle to be valid.

To learn more about triangle

https://brainly.com/question/28470545

#SPJ1

False. For two triangles to be similar, the angles must be equal. The angles of the two triangles given do not match, so the triangles are not similar.

An angle is a geometrical figure that is formed by two lines or rays that have a common endpoint. It is a measure of the amount of turn between the two lines or rays. Angles are typically measured in degrees, with a full angle measuring 360 degrees. Angles can also be measured in radians, with a full angle measuring 2π radians. Angles are used in math and science to describe position and orientation. Common examples of angles include right angles, acute angles, obtuse angles, and straight angles. Angles can be used to calculate the area of polygons, measure the slope of a line, and determine the force of friction.

To learn more about angle
https://brainly.com/question/25716982
#SPJ1

Complete Question:
A triangle has angles that measure 45° and 65°. A second triangle has angles that measure 110° and 30°. These two triangles are similar. O True O False

The οutput axis is independent οf what the input is, as the slοpe is zerο in the graph.

A graph is a structure made up οf a cοllectiοn οf things, where sοme οbject pairs are cοnceptually "cοnnected." The items are represented by mathematical abstractiοns knοwn as vertices, and each pair οf cοnnected vertices is referred tο as an edge.

Here the given :

The graph belοw was drawn with οutput οn the vertical axis and input οn the hοrizοntal axis,

⇒ Slοpe = 0 (can be seen frοm graph),

Frοm the graph, y = 4 is the graph's equatiοn, and the slοpe οf the graph is zerο. The result will always be the same, regardless οf the input. Because the οutput is unifοrm thrοughοut, the input dοesn't really care what happens tο it.

Therefοre, the οutput axis is independent οf what the input is, as the slοpe is zerο in the graph.

To learn more about graph refer the below link

https://brainly.com/question/10712002

#SPJ1

The total derivative of a function is not necessarily one-to-one. The total derivative represents the change in a function with respect to all of its input variables.

If a function has multiple input variables, the total derivative is a matrix, called the Jacobian matrix, whose entries represent the partial derivatives of the function with respect to each input variable.

A function with a non-invertible Jacobian matrix is not one-to-one, since multiple input values can result in the same output value. For example, consider the function f(x,y) = (x^2, y^2). The total derivative of f is given by the Jacobian matrix:

| 2x 0 |

| 0 2y|

This matrix is non-invertible when x=0 or y=0, since it has a determinant of zero. Thus, the function f is not one-to-one when x=0 or y=0.

In terms of polynomials, the total derivative is important for determining whether a polynomial has multiple roots. A root of a polynomial is a value of the input variable that causes the polynomial to equal zero. If a polynomial has multiple roots, it is not one-to-one, since different input values can result in the same output value.

The total derivative of a polynomial can be computed using the power rule of differentiation. For example, consider the polynomial p(x) = x^3 - 6x^2 + 11x - 6. The total derivative of p with respect to x is:

p'(x) = 3x^2 - 12x + 11

If p'(x) has multiple roots, then p(x) has multiple roots as well. In this case, p'(x) has roots at x=1 and x=11/3, so p(x) has multiple roots at x=1 and x=3. Thus, the total derivative is useful for identifying when a polynomial is not one-to-one.

To know more about one-to-one function click here:

brainly.com/question/18154364

#SPJ4

Is total derivative  is one-to-one? explain the significance of this result in terms of the derivative on polynomials.

Answer:

Step-by-step explanation:

Simplifying the expression resulted to x° = x

The expression x° = ½ • (30 + 2x – 30) can be simplified as follows:

The term 30 - 30 simplifies to 0, so we can remove it from the expression:

x° = ½ • (30 + 2x - 30)

x° = ½ • (2x)

We can simplify the fraction ½ by dividing the numerator by the denominator:

x° = x

Therefore, the solution to the equation x° = ½ • (30 + 2x – 30) is x = x°. In other words, any value of x is equal to its corresponding value in degrees.

Learn more about simplifying at:

https://brainly.com/question/28595186

#SPJ1

A sample size of at least 61 should be taken to obtain a margin of error of 0.04 for the estimation of a population proportion at a 95% confidence level.

Given data:

To determine the sample size required for estimating a population proportion with a given margin of error at a 95% confidence level, you can use the following formula:

[tex]n=\frac{Z^2 \cdot p(1-p)}{E^2}[/tex]

n is the required sample size.

Z is the Z-score corresponding to the desired confidence level. For a 95% confidence level, the Z-score is approximately 1.96.

p is an estimate of the population proportion (since you don't have prior data, you can use p =0.5  for maximum variability, which results in the largest sample size requirement).

E is the desired margin of error, which is 0.04 in this case.

Substitute the values into the formula:

[tex]n=\frac{1.96^2*0.5^2}{0.04^2}[/tex]

The value of n = 60.26

Since the sample size is a whole number, n = 61

Hence, a sample size of at least 61 should be taken for the estimation of a population proportion at a 95% confidence level.

To learn more about confidence interval, refer:

https://brainly.com/question/16807970

#SPJ12

Here option A is correct: "The change in expected height for every one additional centimeter of femur length."

What is a centimetre?

A centimetre is a metric unit of length equal to one-hundredth of a meter. It is commonly used to measure small distances, such as the length or width of an object.

What is meant by femur length?

Femur length is the measure of the longest bone in the human body, located in the thigh. It is commonly used as an indicator of the overall height and skeletal proportions.

To know more about femur length visit:

brainly.com/question/30887754

#SPJ1

Answer:

25 Per Minute

Step-by-step explanation:

25 X 10 = 250

Hope This Helps! ^^

25 per minute

So if she stamped 250 envelopes in 10 minutes, we have to divide 250 by 10, which equals to 25!

Hope this helps! You just submitted the picture and never really showed which side was a b c or anything!

By the angle bisector theorem,

[tex]\frac{5}{9}=\frac{2}{x-2}[/tex]

After cross multiplying,

5(x-2) = 2(9)

5x-10 = 18

5x = 28

x = 5.6

As a result, there is a about 74.53 degree elevation difference between the ladder and the ground.

A geometric shape known as an angle is created when two rays or line segments come together at a location known as the vertex. The sides of the angle are the rays or line segments. Angles are used to define the amount of rotation or inclination between two lines or planes and are commonly measured in degrees or radians. The most popular unit of measurement for angles is the degree, which is derived from the 360 equal divisions of a circle. Angles are measured in degrees using a protractor, and each component is referred to as a degree.

given

We may resolve this issue using trigonometric functions. The elevation angle between the ladder and the ground will be denoted by the symbol. Next, we have

opposite/hypotenuse of sin()

adjacent/hypotenuse = cos()

The building's height in this instance serves as the opposing side, and the length of the ladder serves as the hypotenuse. We thus have:

height/35 cos() = 9.7/35 sin()

By rearranging the first equation, we can find the height:

height equals 35*sin()

The second equation can then be changed to include the following expression:

cos(θ) = 9.7/35

cos(θ) = 0.2771

By taking the inverse cosine of both sides, we can now solve for :

θ = cos^(-1)(0.2771) (0.2771)

7.453 degrees

As a result, there is a about 74.53 degree elevation difference between the ladder and the ground.

To know more about angles visit:

https://brainly.com/question/14569348

#SPJ1

Answer:

Step-by-step explanation:

From Point 1 to Point 2 on the trail, the bike rider is traveling uphill, which means that the change in kinetic energy is negative because the rider is slowing down due to the work required to move against gravity. The rider is losing kinetic energy and converting it into potential energy.

On the other hand, the change in potential energy from Point 1 to Point 2 is positive because the rider is gaining height and storing potential energy due to the work done against gravity. As the rider climbs uphill, the potential energy of the rider-bike system increases.

So, to summarize:

Change in kinetic energy from Point 1 to Point 2: Negative

Change in potential energy from Point 1 to Point 2: Positive

Answer:

1 hours and 55 minute?

Step-by-step explanation:

The exponential function that shows the relationship between the city's population y and the number of years t since the start of the study is [tex]y = 390000 * (1.073)^t[/tex]

Population tends to change with time. It might increase or decrease. Let y be the city's population after t years since the start of the study, and let [tex]Po[/tex] be the initial population at the start of the study. We can use the formula for exponential growth to represent the relationship between y and t:

Final population = Initial population x (growth rate)^years

[tex]y = Po*(1+0.073)^t[/tex]

[tex]y = Po* (1.073)^{(t)[/tex]

Substituting the values in the above equation we get the following equation:

[tex]y = 390,000*(1.073)^t[/tex]

The above function when represented in exponential form will be equal to [tex]y=390,000*(e)^{(0.073t)[/tex]

Learn more about Exponential function at:

brainly.com/question/2456547

#SPJ4

Refer to complete question below:

At the beginning of a population study, a city had 390,000 people. Each year since, the population has grown by 7.3% . Let t be the number of years since start of the study. Let y be the city's population. Write an exponential function showing the relationship between y and t .

The next two terms in this arithmetic progression is 7.60 and 7.61.

An arithmetic prοgressiοn (AP) is a sequence where the differences between every twο cοnsecutive terms are the same. Fοr example, the sequence 2, 6, 10, 14, … is an arithmetic prοgressiοn (AP) because it fοllοws a pattern where each number is οbtained by adding 4 tο the previοus term. A real-life example οf an AP is the sequence fοrmed by the annual incοme οf an emplοyee whοse incοme increases by a fixed amοunt οf $5000 every year.

We know the Arithmetic progression formula:

[tex]\rm a_{n}=a_{1}+(n-1)d[/tex]

[tex]\rm a_n[/tex] = the nᵗʰ term in the sequence

[tex]\rm a_1[/tex] = the first term in the sequence

d = the common difference between terms

Here 4 terms are given

5th and 6th terms are to be found,

Thus,

a₁ = 9.56

d = (9.56 -9.57) = 0.01

n = 5

Then

5th term is :

aₙ = a₁ + (n - 1)d

aₙ = 9.56 + (5 - 1)0.01

aₙ = 9.56 + (4)0.01

aₙ = 9.56 + 0.04

aₙ = 7.60

6th term is :

aₙ = a₁ + (n - 1)d

aₙ = 9.56 + (6 - 1)0.01

aₙ = 9.56 + (6)0.01

aₙ = 9.56 + 0.05

aₙ = 7.61

Thus, The next two terms in this arithmetic progression is 7.60 and 7.61.

Learn more about arithmetic prοgressiοn

https://brainly.com/question/30364336

#SPJ1

Answer:

We can check which dimensions are possible for the rectangle by finding the product of the width and length and seeing if it equals the given area of (24x + 30) square units.

Let's check each option:

width 6 units; length (4x + 5) units

Area = 6(4x + 5) = 24x + 30

This option is possible.

width 4 units; length (6x + 7) units

Area = 4(6x + 7) = 24x + 28

This option is not possible since the area is not equal to (24x + 30).

width 3 units; length (21x + 27) units

Area = 3(21x + 27) = 63x + 81

This option is not possible since the area is not equal to (24x + 30).

width 8 units; length (3x + 4) units

Area = 8(3x + 4) = 24x + 32

This option is not possible since the area is not equal to (24x + 30).

width 2 units; length (15 + 12x) units

Area = 2(15 + 12x) = 30 + 24x

This option is not possible since the area is not equal to (24x + 30).

Therefore, the only possible dimension for the rectangle is width 6 units and length (4x + 5) units.

the receiver is located at (0, 0, 2.25 feet) or (0, 0, 27 inches).To find the location of the receiver, we first need to determine the equation of the paraboloid.

The standard equation for a paraboloid of revolution with a vertical axis is:

z = [tex](x^2 + y^2)[/tex]/(4f)

Where:

z is the height at any point (x, y) on the paraboloid.

x and y are the horizontal coordinates of the point.

f is the focal length of the paraboloid, which is half the depth of the dish.

In this case, the dish is 6 feet across at its opening, so the diameter is 6 feet and the radius is 3 feet. Therefore, the maximum value of x and y is 3 feet. The depth of the dish is given as 2 feet.

Using these values, we can solve for the focal length:

2 = [tex](3^2 + 3^2)[/tex]/(4f)

2 = 18/(4f)

f = 18/8 = 9/4 = 2.25 feet

Now that we have the value of f, we can find the location of the receiver, which is placed at the focus of the paraboloid. The focus is located at (0, 0, f).

Therefore, the receiver is located at (0, 0, 2.25 feet) or (0, 0, 27 inches).

Learn more about equation here

https://brainly.com/question/29657992

#SPJ4

The child should be given 15 ml of the medicine to receive 300 mg of the active ingredient.

The given problem requires us to determine the number of milliliters of a liquid medicine that a child should receive in order to obtain a specific dosage of the active ingredient. We are given that the medicine contains 100 mg of the active ingredient in 5 ml.

The child needs to receive 300 mg of the active ingredient, and there are 100 mg of the active ingredient in 5 ml of the medicine. Therefore, the child should be given:

[tex]\frac{300 mg}{100mg/5ml} = \frac{300\text{ mg} \times 5\text{ ml}}{100\text{ mg}} = 15\text{ ml}$$[/tex]

So the child should be given 15 ml of the medicine to receive 300 mg of the active ingredient.

Learn more about Liquid Measurements:

https://brainly.com/question/7744911
#SPJ4

The distribution described is a binomial distribution.

A binomial distribution describes a discrete probability distribution, which means the values are countable. This distribution has two possible outcomes, in this case, either a girl or a boy. The probability of getting a girl is 0.5, as there are 10 girls and 10 boys in the group.

The binomial distribution is described by the following formula: P(x) = nCx * p^x * (1-p)^n-x, where n is the number of trials, x is the number of successes, and p is the probability of success in each trial.

In this case, n=5, x= number of girls, and p=0.5. Thus, P(x)= 5Cx * 0.5^x * 0.5^5-x. To predict the number of girls among 5 randomly selected children from the group, we need to calculate P(x) for x=0,1,2,3,4, and 5. This will give us the probabilities of selecting 0, 1, 2, 3, 4, and 5 girls in the group.

The sum of all these probabilities should be equal to 1, indicating that all the possibilities have been accounted for. This binomial distribution will help us predict the number of girls among 5 randomly selected children from the group of 10 girls and 10 boys.

To know more about  binomial distribution refer here:

https://brainly.com/question/14565246

#SPJ11

Except than x = 1, all real numbers fall within the function's domain.

Since there are no limitations on what we can substitute for x, the domain of a function, f(x), is all real numbers because any real numbers would make f(x) a defined function. As a result, when this is not the case, the domain of a function, f(x), is not all real numbers.

The rational function r(x) = 2x/(x-1) is defined as follows.

So, we set the denominator to zero and solve for x in order to determine the domain of r(x):

x - 1 = 0

x = 1

Hence, x = 1 is the only value of x that causes the denominator to equal 0. R(x) therefore has a domain of all real numbers other than x = 1.

We can express the domain as follows in interval notation:

(-∞, 1) U (1, ∞)

Except than x = 1, all real numbers fall within the function's domain.

To know more about function visit:-

https://brainly.com/question/14830166

#SPJ1

Question:

Which of the following correctly describes the domain of the function shown below?

r(x) = 2x x-1

A. {x:x0}

B. {x: x = 1}

c. x all .real .numbers}

D. xx1}

There are 35 different 3-digit numbers that can be formed using the digits 0, 1, 2, 3, 4, 5, 6, if the repetition of digits is not allowed.

Probability is a branch of mathematics that deals with the study of randomness and uncertainty in events. It is the measure of the likelihood or chance that an event will occur. Probability is expressed as a number between 0 and 1, where 0 indicates that the event will not occur and 1 indicates that the event will occur with certainty.

To form a 3-digit number using the given set of 7 digits (0, 1, 2, 3, 4, 5, 6) without repetition, we need to choose 3 different digits from the set.

We can count the number of ways to select 3 distinct digits from the set of 7 using the combination formula, which is:

C(n, k) = n! / (k! * (n-k)!)

Where n is the total number of items in the set, and k is the number of items we want to choose.

In this case, n = 7 (because we have 7 digits to choose from), and k = 3 (because we want to choose 3 digits to form a 3-digit number).

Therefore, the number of ways to select 3 distinct digits from the set of 7 is:

C(7, 3) = 7! / (3! * 4!)

= (7 * 6 * 5 * 4 * 3 * 2 * 1) / ((3 * 2 * 1) * (4 * 3 * 2 * 1))

= (7 * 6 * 5) / (3 * 2 * 1)

= 35

Therefore, there are 35 different 3-digit numbers that can be formed using the digits 0, 1, 2, 3, 4, 5, 6, if the repetition of digits is not allowed.

To know more about probability visit :

https://brainly.com/question/13604758

#SPJ1

The three numbers are 50, 50, and 50, which give a maximum sum of products taken two at a time of 5000.

To find the sum of three numbers whose product is maximum, we need to distribute the numbers as equally as possible. Therefore, we divide 150 by 3, giving 50. This means that the sum of the three numbers is 150, and their product is maximized.

To check that this is indeed the case, we can calculate the sum of the products taken two at a time: 50x50 + 50x50 + 50x50 = 5000, which is the maximum possible sum.

Therefore, the three numbers are 50, 50, and 50.

To know more about sum of products, refer here:

https://brainly.com/question/4523199#

#SPJ11

The probability that a bridge hand includes 4 acres and exactly 3 kings is 0.028%

To find the probability of getting exactly 4 aces and 3 kings in a bridge hand, we can use the following formula:

P(4 aces and 3 kings) = (number of ways to get 4 aces and 3 kings) / (number of ways to select 13 cards from a deck of 52)

To calculate the numerator, we can first find the number of ways to choose 4 aces from the 4 available in the deck, and then the number of ways to choose 3 kings from the 4 available in the deck. The remaining 6 cards can be any of the 44 non-ace, non-king cards. Therefore:

Number of ways to get 4 aces and 3 kings = (4 choose 4) x (4 choose 3) x (44 choose 6) = 1 x 4 x 44,380,776 = 177,523,104

To calculate the denominator, we can find the total number of ways to choose any 13 cards from the 52-card deck:

Number of ways to select 13 cards from a deck of 52 = (52 choose 13) = 635,013,559,600

Therefore, the probability of getting exactly 4 aces and 3 kings in a bridge hand is:

P(4 aces and 3 kings) = (number of ways to get 4 aces and 3 kings) / (number of ways to select 13 cards from a deck of 52) = 177,523,104 / 635,013,559,600 = 0.0002799 or approximately 0.028%.

To know more about the "probability": https://brainly.com/question/24756209

#SPJ11

Answer:

[tex]y = \frac{2}{7} x - \frac{20}{7} [/tex]

Step-by-step explanation:

[tex] - 2 = \frac{2}{7} (3) + b[/tex]

[tex] - \frac{14}{7} = \frac{6}{7} + b [/tex]

[tex]b = - \frac{20}{7} [/tex]

[tex] y = \frac{2}{7} x - \frac{20}{7} [/tex]

Answer:

EF = 6.49

FG = 3.96

Step-by-step explanation:

We can solve this problem using sine rule, sine rule states that in a triangle ABC, we have

[tex]\dfrac{BC}{\sin a} = \dfrac{AB}{\sin c} = \dfrac{AC}{\sin b}[/tex]

applying this to our question,

[tex]\dfrac{EG}{\sin 86} = \dfrac{FG}{\sin 39} = \dfrac{EF}{\sin 55}[/tex]

hence,

[tex]FG = \dfrac{EG \sin 39}{\sin 86}[/tex]

[tex]EF = \dfrac{EG \sin 55}{\sin 86}[/tex]

calculating we get,

FG = 3.96

EF = 6.49

Hopefully this answer helped you!!!