Answers
Answer:
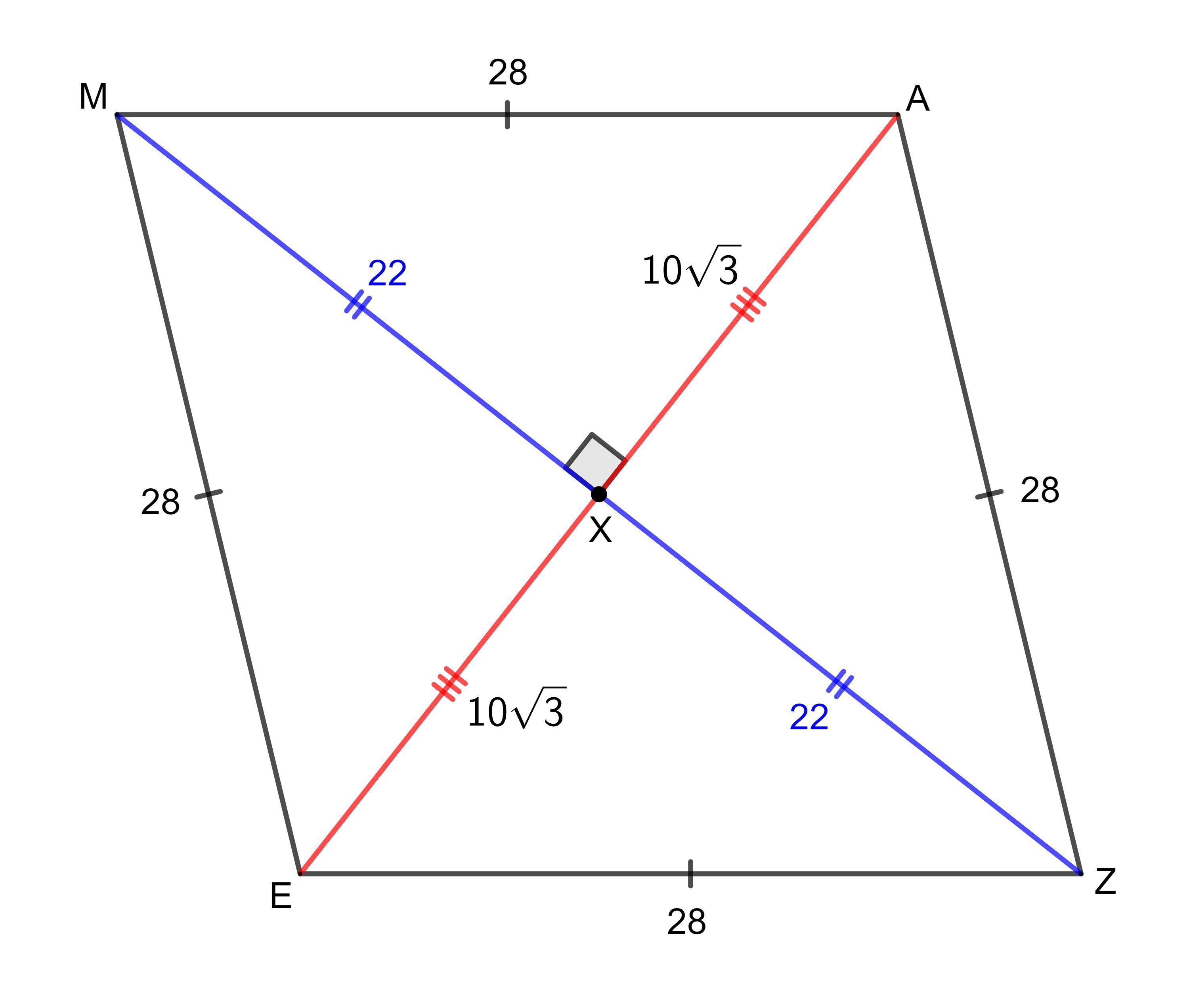
[tex]\textsf{1.}\quad \sf \overline{AZ} = 28 \; meters[/tex]
[tex]\textsf{2.}\quad \sf \overline{AM} = 28 \; meters[/tex]
[tex]\textsf{3.}\quad b = \sf 4[/tex]
[tex]\textsf{4.}\quad \sf Perimeter = 112\; meters[/tex]
[tex]\textsf{5.}\quad \sf \overline{MX} = 22\; meters[/tex]
[tex]\textsf{6.}\quad \sf \overline{AX} = 10\sqrt{3}\; meters[/tex]
[tex]\textsf{7.}\quad \sf \overline{EX} = 10\sqrt{3}\; meters[/tex]
[tex]\textsf{8.}\quad \sf \overline{AE} = 20\sqrt{3}\; meters[/tex]
Step-by-step explanation:
Side lengths and value of bAll sides of a rhombus are the same length. Therefore, for rhombus MAZE:
[tex]\sf \overline{AZ} = \overline{AM} = \overline{ZE} = \overline{EM}[/tex]
Given:
[tex]\overline{\sf AZ} =8b-4[/tex][tex]\overline{\sf AM} =5b+8[/tex]As the sides of a rhombus are the same length, we can equate the expressions for sides AZ and AM, and solve for b:
[tex]\begin{aligned}\overline{\sf AZ}&=\overline{\sf AM}\\8b-4&=5b+8\\8b-4-5b&=5b+8-5b\\3b-4&=8\\3b-4+4&=8+4\\3b&=12\\3b \div 3&=12 \div 3\\b&=4\end{aligned}[/tex]
Therefore, the value of b is 4.
To find the length of AZ and AM, substitute the found value of b into one of the expressions:
[tex]\begin{aligned}\overline{\sf AZ}&=8b-4\\&=8(4)-4\\&=32-4\\&=28\end{aligned}[/tex]
Therefore, as AZ = AM, then AZ = 28 and AM = 28.
[tex]\hrulefill[/tex]
PerimeterAs the sides of a rhombus are equal in length, each side length is 28 meters (as found previously).
The perimeter of rhombus MAZE is the sum of its side lengths. Therefore:
[tex]\begin{aligned}\sf Perimeter\;MAZE&=\sf \overline{AZ} +\overline{AM} +\overline{ZE}+ \overline{EM}\\&=28+28+28+28\\&=112\; \sf meters\end{aligned}[/tex]
Therefore, the perimeter of rhombus MAZE is 112 meters.
[tex]\hrulefill[/tex]
DiagonalsThe point of intersection of the diagonals of rhombus MAZE is point X.
As the diagonals of a rhombus are perpendicular bisectors of each other, then:
[tex]\sf \overline{AX}=\overline{EX}\quad and \quad \overline{AX}+\overline{EX}=\overline{AE}[/tex]
[tex]\sf\overline{MX}=\overline{ZX}\quad and \quad\overline{MX}+\overline{ZX}=\overline{MZ}[/tex]
Given MZ = 44 meters, and MX is half of MZ, then:
[tex]\sf \overline{MX}=\overline{ZX}=22\;meters[/tex]
As the diagonals bisect each other at 90°, m∠MXA= 90°. Therefore, ΔMXA is a right triangle with hypotenuse AM = 28 and leg MX = 22.
As we know the lengths hypotenuse AM and leg MX, we can use Pythagoras Theorem to calculate the length of the other leg, AX:
[tex]\begin{aligned}\sf \overline{AX}^2+\overline{MX}^2&=\sf \overline{AM}^2\\\sf \overline{AX}^2+22^2&=\sf 28^2\\\sf \overline{AX}^2&=\sf 28^2-22^2\\\sf \overline{AX}&=\sqrt{\sf 28^2-22^2}\\\sf \overline{AX}&=\sf 10\sqrt{3}\; meters\end{aligned}[/tex]
As the diagonals bisect each other, AX = EX. Therefore:
[tex]\sf \overline{EX}=\sf 10\sqrt{3}\; meters[/tex]
The length of diagonal AE is the sum of segments AX and EX. Therefore:
[tex]\begin{aligned}\sf \overline{AE}&=\sf \overline{AX}+\overline{EX}\\&=\sf 10\sqrt{3}+10\sqrt{3}\\&=\sf 20\sqrt{3}\; meters\end{aligned}[/tex]
[tex]\hrulefill[/tex]
Note: The attached diagram is drawn to scale.
Related Questions
The Gordon family plans to buy a TV. One TV has a purchase price of $330 and an estimated yearly operating cost of $14. The other has a purchase price of $369 and an estimated yearly operating cost of $9. Which TV should the Gordons buy if they plan to keep it for 8 years? Use rational functions to help justify your answer.
ANSWER:rational functions that model the average annual cost of each television if it is owned for x years, such as f(x)= (330+14x)/x and
g(x)= (369+9x)/x
calculation proving that over 8 years, the annual cost for the $330 television is $55.25; for the $369 television, it is $55.13
statement that the Gordons should buy the $369 television because it is less expensive overall
step by step: edge 2023
Answers
Answer:
The Gordon's should buy TV2
Step-by-step explanation:
To determine which TV the Gordons should buy, we need to compare the total cost of each TV over the 8-year period. Let's define some variables:
- Let x be the number of years the TV is used.
- Let y1 be the total cost of TV 1 over x years.
- Let y2 be the total cost of TV 2 over x years.
- Let P1 be the purchase price of TV 1.
- Let P2 be the purchase price of TV 2.
- Let O1 be the annual operating cost of TV 1.
- Let O2 be the annual operating cost of TV 2.
Using these variables, we can write the following equations:
y1 = P1 + x * O1
y2 = P2 + x * O2
To compare the total cost of each TV over 8 years, we need to find y1 and y2 when x = 8. Plugging in the given values, we get:
y1 = 330 + 8 * 14 = 462
y2 = 369 + 8 * 9 = 441
Therefore, the total cost of TV 1 over 8 years is $462, and the total cost of TV 2 over 8 years is $441. Since TV 2 has the lower total cost, the Gordons should buy TV 2.
From a mathematical standpoint, we can also use rational functions to analyze this problem. The total cost of each TV is a linear function of x, so we can write:
y1(x) = P1 + x * O1
y2(x) = P2 + x * O2
The ratio of these functions is:
y1(x) / y2(x) = (P1 + x * O1) / (P2 + x * O2)
To determine which TV is cheaper over 8 years, we need to compare the ratios when x = 8:
y1(8) / y2(8) = (330 + 8 * 14) / (369 + 8 * 9) ≈ 1.051
Since this ratio is greater than 1, TV 1 is more expensive than TV 2 over 8 years. Therefore, the Gordons should buy TV 2.
Angela, Breanna, Christine, Debbie, and Esther are in a club and they need to pick two people to go to a
meeting. They write each person’s name on equally sized pieces of paper, put them in a hat, and mix the
papers thoroughly. Find the probability model for this chance process and use it to determine the probability
that Angela gets to go to the meeting.
Answers
The probability that Angela gets to go to the meeting is 2/5 or 0.4.
What is probability?
There are a total of 5 people in the club, and they need to pick 2 people to go to the meeting. The number of ways to pick 2 people out of 5 is given by the binomial coefficient:
C(5,2) = 5! / (2! (5-2)!) = 10
This means there are 10 equally likely outcomes, which can be represented by the following probability model:
Outcome Angela goes to meeting? Probability
A,B Yes 1/10
A,C Yes 1/10
A,D Yes 1/10
A,E Yes 1/10
B,C No 1/10
B,D No 1/10
B,E No 1/10
C,D No 1/10
C,E No 1/10
D,E No 1/10
The probability that Angela gets to go to the meeting is the sum of the probabilities of the outcomes where Angela goes to the meeting:
P(Angela goes to meeting) = P(A,B) + P(A,C) + P(A,D) + P(A,E)
= 1/10 + 1/10 + 1/10 + 1/10
= 4/10
= 2/5
Therefore, the probability that Angela gets to go to the meeting is 2/5 or 0.4.
To know more about the probability, visit:
https://brainly.com/question/11234923
#SPJ1
How many feet does Ava walk in one second
Answers
Ava walks 2.5 feet in one second.
How do we calculate?Ava walks 5 feet in 2 seconds, which means that the ratio of feet to seconds is 5 to 2.
We will use proportionality concept , to find out how many feet Ava walks in one second,
Let x be the number of feet Ava walks in one second. Then we can set up the proportion:
5 feet / 2 seconds = x feet / 1 second
solving for x, we can cross-multiply:
5 feet * 1 second = 2 seconds * x feet
Simplifying, we get:
5 feet = 2x feet
Dividing both sides by 2, we get:
x = 2.5 feet
In conclusion, Ava walks 2.5 feet in one second.
Learn more about proportionality concept at: https://brainly.com/question/14060657
#SPJ1
Complete question:
. Ava is walking at a constant speed where for every 5 feet it takes 2 seconds. So, the ratio of feet to seconds is 5 to 2.
(c) How many feet does Ava walk in one second?
The vertices of figure PQRS are translated to form figure P'Q'R'S'. Select all the statements that describe the two figures. Q S R P' S' Q' 'R
the anawer choices are : A. P Q R S is the preimage of PQRS, B. the two figures are congruent, C. the two figures are in different positions , but have the same orientation, D. the two figures are in different positions and have oppsoite orientation , E. corresponding angles and sides of the figures have the same measures.
Answers
The true statements are:
(B) Both figures are congurent.
(C) The two figures have the same orientation but different positions.
(E) Corresponding angles and sides have the same measures.
What is orientation?In geometry, how an item is positioned in the space it occupies—such as a line, plane, or rigid body—is described in terms of its orientation, angular position, attitude, bearing, and direction.
It refers more particularly to the fictitious rotation required to shift an object from a reference placement to its present location.
To get to the current positioning, a rotation might not be sufficient.
It could be required to include a fictitious translation known as the object's location (or position, or linear position).
Together, the position and orientation completely explain where the object is situated in space.
Therefore, the true statements are:
(B) Both figures are congurent.
(C) The two figures have the same orientation but different positions.
(E) Corresponding angles and sides have the same measures.
Know more about orientation here:
https://brainly.com/question/3520971
#SPJ1
Rewrite 1 + 2i in polar form.
A.√5
B.√5∠116.6°
C.[5√∠63.4°]
D.5√∠(63.4°)
Answers
1 + 2i in polar form is 5√2∠63.4°.
What is a polar form ?
In mathematics, the polar form is a way of representing complex numbers using their magnitude and angle. A complex number can be represented in the form r(cos θ + i sin θ), where r is the magnitude (or modulus) of the complex number, and θ is its argument (or phase angle). Alternatively, the polar form can be represented in terms of magnitude and angle as r ∠θ, where r is the magnitude and θ is the angle in radians. This form is also known as the exponential form of a complex number. The polar form is useful in calculations involving complex numbers, especially in multiplication and division, where it is often easier to work with the polar form rather than the rectangular form (a + bi).
D. 5√2∠63.4°
To convert a complex number from rectangular form to polar form, we use the following formulas:
r = √(a^2 + b^2)
θ = tan^-1 (b/a)
Where a and b are the real and imaginary parts of the complex number, respectively.
In this case, a = 1 and b = 2, so:
r = √(1^2 + 2^2) = √5
θ = tan^-1 (2/1) = 63.4°
Therefore, 1 + 2i in polar form is 5√2∠63.4°.
To know more about polar form and given link below -
https://brainly.com/question/11741181
#SPJ1
Use a horizontal or vertical number line. Plot points at 7/10 and it's opposite. Label each point with it's value.
Answers
Answer:
Assuming a vertical number line:
- Plot the point at 7/10 above the origin, between 0 and 1.
- Plot the opposite of 7/10 by reflecting it across the origin to the point at -7/10 below the origin, between 0 and -1.
- Label the point at 7/10 as "7/10" and the point at -7/10 as "-7/10".
The number line would look like this:
1
|
|
|
|
| 7/10
|
|
|
|
0
|
|
|
|
|
| -7/10
|
|
|
|
-1
The circle below is divided into six equal pieces. If the area of the shaded region is 98pi what is the
circumference of the circle? Leave answer in terms of pi
Answers
Consequently, the circle's diameter is 28π√3.
What is its the circumference?The radius of a circular or other curved geometry form refers to its length. It is the border across any two-dimensional circle surface measured linearly in one dimension.
Since the circle is divided into six equal pieces, the shaded region represents one-sixth of the total area of the circle. Therefore, the total area of the circle can be found by multiplying the shaded area by 6:
Total area of circle = 6 × 98π = 588π
The formula for the area of a circle is A = πr², where r is the radius of the circle. Solving for r, we get:
r² = A / π = 588π / π = 588
r = √588 = 2√147 = 2√3 × √49 = 14√3
C = 2r is the method for calculating a circle's diameter. Plugging in the value of r, we get:
C = 2π(14√3) = 28π√3
Therefore, the circumference of the circle is 28π√3.
To know more about Circumference visit:
https://brainly.com/question/20489969
#SPJ1
Scott took out a 72 month
loan for $35,000 to purchase
a new boat. If Scott paid
$8,925 in simple interest,
what was the interest rate?
Answers
$8,925 / ($35,000 * 6 years) = 0.0429 or 4.29%
Therefore, the interest rate on Scott's loan was 4.29%.
The interest rate paid by Scott is 4.25% for the 72 months.
We can determine the simple interest of the given problem by the simple interest formula which is given as :
I=PRT
Where,
I=Interest
P=principal
R=rate in decimal
T=time in years
Converting the given 72 months into years we get time t :
1 year = 12months
72 months / 12months = 6 years
t=6
From the given data
I=8925
P=35000
R=r
T=6
Substituting the above values in the simple interest equation we get:
8925 = 35000*r*6
8925 = 210000*r
divide both sides by 210000
R = 0.0425
Therefore, the interest rate is 4.25%
To learn more about the simple interests :
https://brainly.com/question/25793394
A sector of a circle with a radius of 11 feet has a central angle measure of 15°.
What is the area of the sector rounded to the nearest tenth?
Use 3.14 for π .
52.5 ft 2
31.7 ft2
16.2 ft 2
15.8 ft2
Answers
Answer:
The area of a sector can be calculated using the formula:
A = (θ/360)πr^2
where θ is the central angle measure in degrees, r is the radius, and π is the mathematical constant pi.
Substituting the given values, we get:
A = (15/360)π(11)^2
≈ 16.2 ft^2
Rounding this to the nearest tenth gives:
A ≈ 15.8 ft^2
Therefore, the area of the sector rounded to the nearest tenth is 15.8 ft^2.
Step-by-step explanation:
hope its help <:
Write an expression describing all the angles that are coterminal with 8°. (Please use the variable k in your answer. Give your answer in degrees, but do not include a degree symbol in your answer.)
Answers
the expression describing all the angles that are coterminal with 8° is: θ = 8° + 360°k, where k is an integer.
How to solve and what is angle?
An angle of 8° has an initial side on the positive x-axis and rotates counterclockwise by 8°.
Any angle coterminal with 8° can be expressed as:
θ = 8° + 360°k
where k is an integer.
Therefore, the expression describing all the angles that are coterminal with 8° is:
θ = 8° + 360°k, where k is an integer.
An angle is a geometric figure formed by two rays, called the sides of the angle, that share a common endpoint, called the vertex of the angle. Angles are typically measured in degrees or radians and are used to measure the amount of rotation or turn between two intersecting lines or planes.
To know more about angle related question visit:
https://brainly.com/question/28451077
#SPJ1
MAKE CONNECTIONS Determine whether triangle XYZ can be a right triangle. Explain.
X (0, 0), Y (2h, 2h), Z (4h, 0)
Slope of XY Select Choice -1, 1, or 0
slope of YZ Select Choice 1, 0, or -1slope of ZX Select Choice -1, 1, or 0because Select Choice 1(1) = 1, 1(-1) = -1, 1(0) = 0, or 0(-1) =0XY Select Choice is or is not
perpendicular to YZ. Therefore, triangle XYZ Select Choice is not or is a right triangle.
Answers
Answer: slope of XY is not perpendicular to YZ. Therefore, triangle XYZ is a right triangle.
Step-by-step explanation:
The slope of a line passing through two points (x1, y1) and (x2, y2) is given by (y2 - y1) / (x2 - x1).
Using this formula, we can find the slopes of the three sides of triangle XYZ:
Slope of XY = (2h - 0) / (2h - 0) = 1
Slope of YZ = (0 - 2h) / (4h - 2h) = -h / h = -1
Slope of ZX = (0 - 0) / (4h - 0) = 0
Therefore, the slope of XY is 1, the slope of YZ is -1, and the slope of ZX is 0.
Since the product of the slopes of two perpendicular lines is -1, we can see that the slope of XY and the slope of YZ are negative reciprocals of each other, which means that they are perpendicular. Therefore, triangle XYZ is a right triangle.
50 POINTS + BRAINLIEST!!!
I have two fair dice each numbered 1 to 6. I am going to throw the two dice. What is the probality that the sum of the numbers of the dice will be a square number?
Answers
Answer:
7/36
Step-by-step explanation:
It is given that we have two dice numbered from 1 to 6 . The maximum sum that can be obtained by rolling two dice is 6+6 = 12 and the minimum sum that can be obtained by rolling is 1+1 = 2 .
Now between 2 and 12 , the numbers which are perfect square are 4 and 9 .
Getting a sum of 4 :-
We can get a sum of four from two dice as ,
1 on first dice, 3 on other.2 on first dice , 2 on other.3 on first dice , 1 on other.Getting a sum of 9 :-
3 on first dice, 6 on other.6 on first dice, 3 on other.4 on first dice, 5 on other.5 on first dice, 4 on other.So there are a total of 7 possibilities by which we can can get a perfect square number by rolling two dices .
Now total number of possible outcomes = 6*6 = 36 .
Henceforth the required probability would be ,
[tex]\rm\implies P( getting \ a \ square\ number) =\dfrac{Total \ number\ of \ favourable\ outcomes}{Total \ number \ of \ possible \ outcomes} [/tex]
[tex]\rm\implies \underline{\underline{\red{ P( getting \ a \ square\ number)=\dfrac{7}{36}}}}[/tex]
Hence the required probability is 7/36 .
The probability of getting a square number as the sum is therefore 7/36.
WHAT IS PROBABILITY ?
Probability is a branch of mathematics that deals with the study of random events or phenomena. It involves analyzing the likelihood of an event occurring, given the conditions or circumstances that surround it. Probability is expressed as a number between 0 and 1, where 0 represents an impossible event and 1 represents a certain event. The probability of an event is determined by dividing the number of favorable outcomes by the total number of possible outcomes. Probability is widely used in many fields, including statistics, physics, finance, engineering, and social sciences, to name a few.
There are 36 possible outcomes when two dice are thrown since each die has 6 possible outcomes.
Let's find the possible outcomes where the sum of the numbers on the dice is a square number. The only possible sums that are squares are 4, 9 and 16.
To get a sum of 4, the dice must land on 1 and 3 or 3 and 1. There are two possible ways of doing this, so there are 2 outcomes.
To get a sum of 9, the dice must land on 3 and 6, 4 and 5, 5 and 4, or 6 and 3. There are four possible ways of doing this, so there are 4 outcomes.
To get a sum of 16, the dice must both land on 6. There is only one possible way of doing this, so there is 1 outcome.
Therefore, there are 2 + 4 + 1 = 7 outcomes where the sum of the numbers on the dice is a square number.
The probability of getting a square number as the sum is therefore 7/36.
To know more about probability visit :-
https://brainly.com/question/13604758
#SPJ1
Under Todd’s new cable television plan, his bill averages $63 per month. This is 140% of his average monthly bill last year when he had the basic cable package. What was his average monthly cable bill last year?
Answers
Answer:
45
Step-by-step explanation:
translation :
140% of x = $63
x = $63 ÷ 1.4
x = $45
FUN FACTS :
interesting: 100% means double that number or times 2
if a price is $20 & it increases 100% in price that means its $20 times 2 or $40
percent means per 100
cent means 100 in latin
that's why the decimal moves 2 spaces
for the 2 zeros in 100
chatgpt
Plastic souvenir cups come in three different sizes: small (S), medium (M), and large( L). The available colors are red R, white W, and blue B. Make a list to represent all the possible combinations of the different cups based on size and color. Write each outcome in the format (Size, Color).
due by tomorrow!!
Answers
The answer of the question based on probability of the representing all the possible combinations of the different cups based on size and color the list is given below,
What is Event?In probability theory, event is set of possible outcomes or results of an experiment or situation. For example, rolling a six-sided die and getting even number is event, as it consists of set of possible outcomes {2, 4, 6}.
Events can also be mutually exclusive or independent. Two events are mutually exclusive if they cannot occur at same time, like rolling a 1 and rolling a 2 on a die.
Events can be simple or compound. A simple event consists of single outcome, like rolling particular number on a die, while compound event consists of more than one outcome, like rolling an even number or rolling number greater than 4 on a die.
Here is a list of all possible combinations of the different cups based on size and color:
Small, Red (S,R)
Small, White (S,W)
Small, Blue (S,B)
Medium, Red (M,R)
Medium, White (M,W)
Medium, Blue (M,B)
Large, Red (L,R)
Large, White (L,W)
Large, Blue (L,B)
There are a total of 9 possible combinations of cup size and color.
To know more about Experiment visit:
https://brainly.com/question/29104118
#SPJ1
The measure of an angle is twice less than that of its supplement angle.
Answers
The supplementary angle will be 60°.
What are supplementary angles?
Supplementary angles are angles (only two) whose sum is equal to 180 degrees. In other words, if we add two angles together and the result is 180 degrees, those angles are considered supplementary.
For example, if we have angle A that measures 60 degrees, its supplement angle B will measure 120 degrees (180 - 60 = 120). Angles A and B are supplementary angles.
Supplementary angles can be adjacent, meaning they share a common vertex and side, or they can be non-adjacent. In either case, their sum will always be 180 degrees.
Supplementary angles are commonly used in geometry and trigonometry to solve problems related to angles and triangles.
Now,
Let x = measure of the angle.
Then, the supplement angle is 180 - x.
According to the problem, x is twice less than the supplement angle. In other words, the supplement angle is twice greater than x. We can write this as:
180 - x = 2x
Solving for x, we get:
180 = 3x
x = 60
Therefore, the angle measures 60 degrees.
To know more about supplementary angles visit the link
brainly.com/question/22960799
#SPJ1
Right Question:- The measure of an angle is twice less than that of its supplement angle. find that angle?
eight times the product of 4 and a number in an algebraic expression, then simplify the expression.
Answers
8(4x)
v
32x
A researcher asked 520 randomly selected people of three different age groups (teen, young adult, and adult) about their favorite music genre. The two-way table displays the distribution of the responses.
A 4-column table with 3 rows. Column 1 has entries country, rock, oldies. Column 2 is labeled Teen with entries 61, 94, 15. Column 3 is labeled young adult with entries 65, 84, 36. Column 4 is labeled Adult with entries 49, 54, 62. The columns are labeled age and the rows are labeled music.
A participant is randomly selected. Let C be the event that the participant prefers country music and let T be the event that the participant is a teen. What is the value of P(C or T)?
0.12
0.33
0.55
0.66
Answers
The probability that the participant either is a teen or prefers country music is given as follows:
P(C or T) = 0.55.
How to calculate a probability?A probability is calculated as the division of the desired number of outcomes by the total number of outcomes in the context of a problem/experiment.
The desired outcomes for this problem are given as follows:
61 + 94 + 15 = 170 teens.65 + 49 = 114 people that are not teens but prefer country music.There were 520 people in the research, hence the probability that the participant either is a teen or prefers country music is given as follows:
P(C or T) = (170 + 114)/520
P(C or T) = 0.55.
More can be learned about probability at https://brainly.com/question/24756209
#SPJ1
(1.8 x 10^8) / (3 x 10^2)
Answers
Friend need help I ain’t doing all dat to solve
Answers
Answer:
1. is 10
2. is 4
3. is 2
?= is 2
Help please I got 5.76 I don’t know if that’s right
Answers
Answer:
trust yourself cuh
Step-by-step explanation:
the front of a tent has the shape of an isosceles triangle with equal sides of 163 cm long. the measure of the angle at the peak of the tent is 103 degrees. determine the height of the tent to the nearest centimetre.
Answers
To find the height of the tent, we need to use trigonometry. Let's draw a diagram to help visualize the problem
/|\
/ | \
h / | \ h
/ | \
/ | \
/ | \
/ | \
/_ _|_ __\
b 81.5 b
We can see that the height of the tent (h) forms one leg of a right triangle, with the base (b) being half of one of the equal sides of the isosceles triangle. We can use the angle at the peak of the tent (103 degrees) to find the height using the tangent function:
tan(103) = h/b
To find b, we can use the fact that the equal sides of the isosceles triangle are 163 cm long, so b = 163/2 = 81.5 cm.
Now we can plug in b and the angle measure into the tangent equation and solve for h:
tan(103) = h/81.5
h = 81.5 * tan(103)
h ≈ 370.5 cm
Therefore, the height of the tent is approximately 370.5 cm or 371 cm to the nearest centimeter.
Find the value of x and y. If your answer is not an integer, leave it in simplest radical form. The diagram is not drawn to scale.
Answers
Step-by-step explanation:
For x;
[tex]{ \tt{ \tan( \theta) = \frac{opposite}{adjacent} }} \\ \\ { \tt{ \tan( 60 \degree) = \frac{x}{5} }} \\ \\ { \tt{x = 5 \tan(60 \degree) }} \\ \\ { \tt{x = 5 \sqrt{3} }}[/tex]
For y;
[tex] { \tt{\cos( \theta) = \frac{adjacent}{hypotenuse} }} \\ \\ { \tt{cos(60 \degree) = \frac{5}{y} }} \\ \\ { \tt{y = 5 \cos(60 \degree) }} \\ \\ { \tt{y = 2.5}}[/tex]
What is the product of 7x(2x-6)
Answers
Answer: 14x(x−3)
Step-by-step explanation:
the diagram shows a 5x5x5 cube calculate the length of the diagonal AB
Answers
Answer:4
Step-by-step explanation:4
A candy dispenser put various numbers of orange candies into bags.
Orange candies per bag
Stem Leaf
2
137
8
78
4
5
6
1248
368
0359
59
How many bags had exactly 27 orange candies?
bags
Answers
The number of bags that had exactly 27 orange candies is given as follows:
Zero.
What is shown by a stem-and-leaf plot?A stem and leaf plot is a type of data visualization that displays numerical data in a way that shows the distribution of the data while also preserving the individual data points. It is particularly useful for small to medium-sized data sets.
In a stem and leaf plot, the digits in each data point are split into two parts: the stem and the leaf. The stem is usually the leftmost digits of the number, while the leaf is the rightmost digit. The stems are listed in a column from top to bottom, and each leaf is listed next to its corresponding stem. The resulting plot looks like a table with two columns, where the first column shows the stems and the second column shows the leaves.
From the plot given at the end of the answer, the measures are given as follows:
20, 22, 22, 22, 32, 33, 37, 37, 39, ..., 59.
As the number 27 does not show up in the data-set, there were zero bags with exactly 27 candies.
Missing InformationThe plot is given by the image presented at the end of the answer.
More can be learned about stem and leaf plots at https://brainly.com/question/8649311
#SPJ1
Ronald likes to skate at a game store that is due south of his school and due west of his favorite skate park. If the game store is 7 miles from his school and the straight line distance between yhe school and the skate park is 8 miles, how far is the game store from the skate park?
Answers
Answer:
15 miles
Step-by-step explanation:
7 miles from game store to school plus another 8 miles from school to skate park equal 15.
Arrange the quantities from smallest to largest. 2.4 dag. , .21 kg , 190 cg
Answers
The quantities arranged from smallest to largest are 1.9 g, 24 g, and 210 g.
What is quantity?A quantity is a property or attribute of an object or phenomenon that can be measured or described numerically. Quantities can be either scalar, meaning they have a magnitude (or size) but no direction, or vector, meaning they have both a magnitude and a direction.
According to question:First, let's convert all the quantities to the same unit.
2.4 dag = 24 g (since 1 dag = 10 g)
0.21 kg = 210 g (since 1 kg = 1000 g)
190 cg = 1.9 g (since 1 cg = 0.01 g)
Now we can arrange the quantities from smallest to largest:
1.9 g
24 g
210 g
Therefore, the quantities arranged from smallest to largest are 1.9 g, 24 g, and 210 g.
Dag is a weight measuring unit that is rarely applied in daily life. Dag is an abbreviation for "dekagram", which is a metric unit of mass equal to 10 grams. One dekagram is equivalent to 0.01 kilograms or 0.3527 ounces.
To know more about quantity visit:
https://brainly.com/question/12986460
#SPJ1
The tens digit in a dividend is less than the divisor. The divisor has one digit. Gracie says the quotient must have a 0 in the tens place. Is Gracie correct? Explain
Answers
Gracie's statement is not necessarily correct about the tens digit in a dividend is less than the divisor and the divisor has one digit. Gracie says the quotient must have a 0 in the tens place.
What is dividend?
In mathematics, a dividend is the number that is being divided in a division problem. For example, in the division problem 18 ÷ 3 = 6, 18 is the dividend.
Gracie's statement is not necessarily correct. Let's look at a couple of examples to see why.
Example 1:
Dividend = 25
Divisor = 4
In this case, the tens digit of the dividend (2) is less than the divisor (4). The quotient is 6 with a remainder of 1. There is no 0 in the quotient, so Gracie's statement is incorrect.
Example 2:
Dividend = 35
Divisor = 4
In this case, the tens digit of the dividend (3) is also less than the divisor (4). The quotient is 8 with a remainder of 3. Again, there is no 0 in the quotient, so Gracie's statement is still incorrect.
From these examples, we can see that Gracie's statement is not always true. It is possible for the tens digit of the dividend to be less than the divisor, and for the quotient to not have a 0 in the tens place.
The only time Gracie's statement would be true is if the remainder is 0 after dividing the dividend by the divisor. In that case, the quotient would indeed have a 0 in the tens place. However, this is not always the case.
To learn more about dividend visit:
https://brainly.com/question/30126004
#SPJ9
type of measurement enables learners to quantify the measurement of an object, but differs in amount each time.
Answers
Answer:
variable measurement
Step-by-step explanation:
The type of measurement you are referring to is called "variable measurement". In variable measurement, the quantity being measured can vary from one observation to another. This means that the measurement is not consistent or fixed, and can change each time it is taken. An example of variable measurement is measuring the weight of a person over time, as their weight can change from one day to another. Another example is measuring the temperature in a room throughout the day, as the temperature can fluctuate based on factors such as sunlight, air conditioning, and human activity.
Makesha lost 58.5 pounds in 18 weeks. Find her rate of loss in pounds per week.
