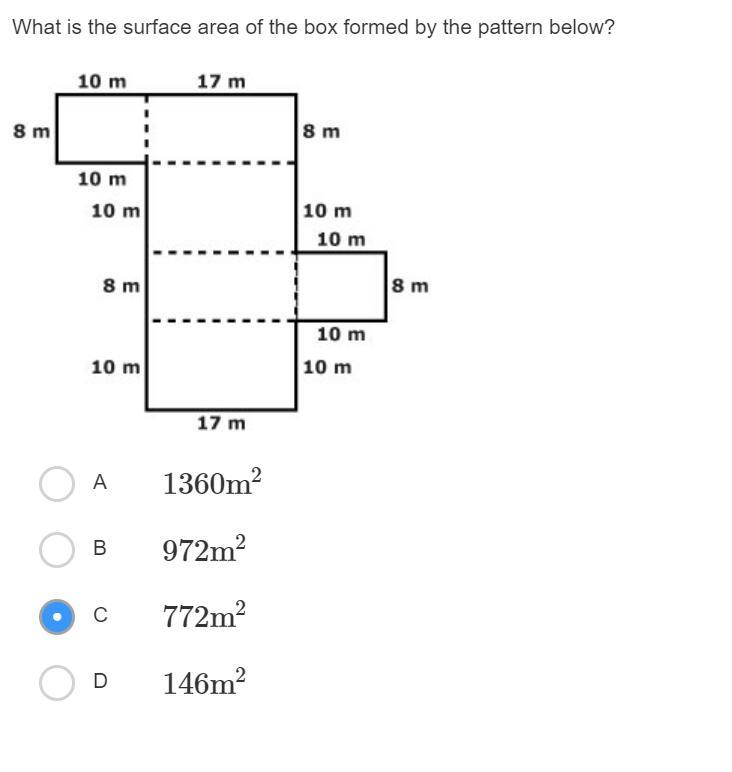
Answers
Answer:772
Step-by-step explanation:
SA=PH+2b
SA=(10+8+10+8)(17)+2(8x10)
SA=772
Answer:
Step-by-step explanatin
multiply all of them
Related Questions
In circle S with m/RST = 56 and RS = 19 units, find the length of arc RT.
Round to the nearest hundredth.
R
S
Answers
In circle S with m∠RST= 56 and RS = 19 units, the length of arc RT ≈ 8.87 units (rounded to two decimal places).
Describe Arc of Circle?An arc of a circle is a portion of the circumference of the circle. It is defined by two endpoints and the collection of all points on the circle's circumference that lie between these endpoints. The length of an arc is proportional to the measure of its corresponding central angle. The formula to find the length of an arc of a circle is L = (m/360) x 2πr, where L is the length of the arc, m is the measure of the central angle, and r is the radius of the circle. The symbol for an arc is a segment of the circle with a curved line over it.
We know that in a circle with radius r, the measure of the arc of a central angle with measure θ degrees is (θ/360) × 2πr units.
In circle S with center S, we are given that RS = ST = r (say) and m∠RST = 56 degrees. So, the measure of minor arc RT is also 56 degrees.
Therefore, the length of arc RT = (56/360) × 2πr = (7/45) × 2πr.
We are also given that RS = 19 units. Since RS = ST = r, we have r = 19 units.
Substituting this value of r, we get:
Length of arc RT = (7/45) × 2πr = (7/45) × 2π(19) ≈ 8.87 units (rounded to two decimal places).
To know more about radius visit:
https://brainly.com/question/15448382
#SPJ1
Answer:
RT= 18.57
Step-by-step explanation:
TRUST THE PROCESS
A 13 ft ladder is leaning against a building. The top of the ladder is 6 ft above the ground.
How far from the building is the ladder?
Enter your answer, rounded to the nearest tenth of a ft,
Answers
Thus, the distance of ladder from the building is found to be 11.53 ft.
Explain about the Pythagorean theorem?Exactly single right angle measure 90 degrees characterises a right triangle.
The hypotenuse of the a right triangle's square is equal to the sum of its other two sides, according to the Pythagorean Theorem. It is written as a²+b²=c² in equation form.
Pythagoras is in the form of;
a²+b²=c²
Let the distance of ladder from the building be 'x'.
Height of ladder from ground h = 6 ft.
Length of ladder l = 13 ft.
Here, using the Pythagorean theorem;
x² + 6² = 13²
x² = 13² - 6²
x² = 169 - 36
x² = 133
x = √133
x = 11.53
Thus, the distance of ladder from the building is found to be 11.53 ft.
Know more about the Pythagorean theorem
https://brainly.com/question/343682
#SPJ1
Select the correct answer.
A graph with a y-axis and an x-axis in positive and negative planes. A figure is formed M F G H I J K L is made by connecting points (-3,5), (8,5), (8,2), (3,2), (3,-5), (-8,-5), (-8,-2), and(-3,-2).
Eleanor is participating in a game show in which she has to complete a lap with seven different obstacles. The lap starts and ends at F. The obstacles are placed at points G, H, I, J, K, L, and M. What is the total length of the lap?
A.
52 units
B.
54 units
C.
56 units
D.
58 units
Answers
Thus, the total length of lap covered to get the seven different obstacles is found as: 52 units.
Define about the distance formula?the Pythagorean theorem is used to calculate the distance between two locations using the distance formula. The Pythagorean theorem can be rewritten as d = √((x2 - x1)²+(y2 - y1)²) to calculate the separation between any two locations.
Given data:
Points on y-axis and an x-axis are given,
M(-3,5), F(8,5), G(8,2), H(3,2), I(3,-5), J(-8,-5), K(-8,-2), and L(-3,-2).
Starting and ending point is F.
Points lies between the starting and ending are-
F ,G, H, I, J, K, L, M, F
Total length = sum of all length
d = √((x2 - x1)²+(y2 - y1)²)
FG = √((8 - 8)²+(2 - 5)²)
FG = √9
FG = 3
GH = √((8 - 3)²+(2 - 2)²)
GH = √25
GH = 5
HI = √((3 - 3)²+(2 + 5)²)
HI = √49
HI = 7
IJ = √((3 + 8)²+(-5 + 5)²)
IJ = √121
IJ = 11
JK = √((-8 + 8)²+(-2 - 5)²)
JK = √9
JK = 3
KL = √((-8 + 3)²+(-2 + 2)²)
KL = √25
KL = 5
LM = √((-3 + 3)²+(-2 - 5)²)
LM = √49
LM = 7
MF = √((8 + 3)²+(+5 - 5)²)
MF = √121
MF = 11
Total length = 3 + 5 + 7 + 11 + 3 + 5 + 7 + 11
Total length = 52 units
Thus, the total length of the lap covered to get the seven different obstacles is found as: 52 units.
know more about the distance formula
https://brainly.com/question/661229
#SPJ1
Each of the designs shown below is to be displayed in a window using strands of white lights. The smaller design requires 225 feet of lights. How many feet of lights does the enlarged design require? Support your answer by showing all work and stating the scale factor used in your solution.
Answers
According to the question the enlarged design requires 450 feet of lights.
What is design?Design is the process of creating a plan or solution to a problem. It involves identifying users’ needs and creating a product, service, or system that meets those needs. Designers must consider how their solutions will function, how it will look, and how people will interact with it. Design thinking is a creative process that involves research, brainstorming, prototyping, and testing. Good design can improve user experience, increase engagement, and help businesses achieve their goals.
Let's assume the original design is X feet.
The enlarged design is 2X feet.
Therefore, the scale factor is 2.
The original design requires 225 feet of lights.
We can use the scale factor to calculate the amount of lights required for the enlarged design.
225 * 2 = 450 feet
Therefore, the enlarged design requires 450 feet of lights.
To learn more about design
https://brainly.com/question/25159431
#SPJ1
Complete Question:
At a graduation dinner, an equal number of guest were seated at each of the 3 large tables, and 7 late arriving guests were seated at a smaller table. There were 37 guests in all. if N represents the number of people seated at each of the large tables, what equation represents the situation.
Answers
Answer:
We know that there were three large tables with an equal number of guests seated at each table. Let's represent the number of guests at each of these large tables with the variable N.
So, the total number of guests seated at the large tables is 3N.
In addition to these guests, there were 7 late arriving guests seated at a smaller table.
Therefore, the total number of guests in all is:
3N + 7
We also know that the total number of guests in all is 37. So we can set up an equation to represent this:
3N + 7 = 37
Simplifying this equation, we get:
3N = 30
Dividing both sides by 3, we get:
N = 10
So, there were 10 guests seated at each of the 3 large tables.
A publisher reports that 75% of their readers own a particular make of car. A marketing executive wants to test the claim that the percentage is actually different from the reported percentage. A random sample of 250 found that 69% of the readers owned a particular make of Car. Find the value of the test statistic. Round your answer to two decimal places
Answers
Rounded to two decimal places, the value of the test statistic is 0.41.
The value of the test statistic to compare the publisher's reported percentage of 75% and the marketing executive's claim that the actual percentage is different can be found by using the formula z = (p1 - p2)/(sqrt[p*(1-p)*((1/n1)+(1/n2))]), where p is the pooled proportion, p1 is the proportion of the publisher's readers owning the particular make of car, p2 is the proportion of the random sample owning the particular make of car, n1 is the total number of the publisher's readers, and n2 is the total number of the random sample.
In this case, p = [tex](75% + 69%)/2 = 72%, p1 = 75%, p2 = 69%, n1[/tex]is unknown, n2 = 250. Thus, the test statistic is z =[tex](75%-69%)/(sqrt[72%(1-72%)((1/n1)+(1/250))]) = 0.41.[/tex]
for such more questions on random sample.
https://brainly.com/question/13219833
#SPJ11
i need help ASAP
Calculate the amount of interest on $2,000.00 for 4 years, compounding daily at 2.25 % APR.
From the Monthly Interest Table use $1.094171 in interest for each $1.00 invested
A $2,088.34
B $2188.34
C $2,288.34
D $2,388.34
Answers
Answer:
Step-by-step explanation:
First, we need to calculate the annual interest rate from the given APR.
APR = 2.25%
Daily interest rate = 2.25% / 365 = 0.00616438
Now, we can use the formula for compound interest:
A = P(1 + r/n)^(nt)
Where:
A = the final amount
P = the principal (initial amount)
r = the annual interest rate (as a decimal)
n = the number of times the interest is compounded per year
t = time in years
In this case, P = $2,000, r = 0.00616438, n = 365 (daily compounding), and t = 4.
A = 2000(1 + 0.00616438/365)^(365*4)
A = 2000(1.00616438)^1460
A = $2,388.34 (rounded to the nearest cent)
Therefore, the answer is option D) $2,388.34.
aldo has scored 77, 88, 77, 87, and 63 on his previous five tests. what score does he need on his next test so that his average (mean) is 79?
Answers
To maintain an average of 79, Aldo must obtain a score of 82 in his upcoming exam.
To get the solution, let's calculate the total of the first five scores.
Total of the first five scores = 77 + 88 + 77 + 87 + 63 = 392
Now we know that there are a total of six scores, so to get the mean, we will divide the total by six.
Mean = Total/Number of ScoresTherefore, 79 = 392 + x/6
We need to find the value of x that will satisfy the above equation.
Now we will solve for x.79 = 392 + x/6
(Multiply both sides by 6) 6 * 79 = 6 * 392 + x6 * 79 = 2352 + xx = 6 * 79 - 392x = 474 - 392x = 82
Therefore, Aldo needs to score 82 on his next test to achieve an average of 79.
To know more about average, refer here:
https://brainly.com/question/15397049#
#SPJ11
What is the value of x given the following image?
Answers
ans- <CDF+<FDE=90(Being right angle)
or, 2x+x+9=90
or, 3x+9=90
or, 3x=90-9
or, 3x=81
or, x=81/3
:.x=27,,
we have 45 m2 of material to build a box with a square base and no top. determine the dimensions of the box that will maximize the enclosed volume.
Answers
The dimensions of the box that will maximize the enclosed volume are l = √(45/2) m and h = (22.5 - l²)/2 m.
To determine the dimensions of the box that will maximize the enclosed volume if we have 45 m² of material to build a box with a square base and no top, we can use the following steps:
Step 1: Write the formula for the volume of the box.V = l²h
Step 2: Write the formula for the surface area of the box.S = 2l² + 4lh
Step 3: Substitute S = 45 m² and simplify.2l² + 4lh = 45 m²l² + 2lh = 22.5 m²h = (22.5 - l²)/2
Step 4: Substitute the value of h in the formula for the volume and simplify.V = l²[(22.5 - l²)/2]V = (22.5l² - l⁴)/2
Step 5: Take the derivative of V with respect to l.dV/dl = 45l - 2l³
Step 6: Set dV/dl = 0 and solve for l.45l - 2l³ = 0l(2l² - 45) = 0l = 0 or l = √(45/2)
Step 7: Determine if the critical point is a maximum or a minimum by taking the second derivative of V with respect to l.d²V/dl² = 45 - 6l²d²V/dl² > 0 for l = √(45/2)
Therefore, the dimensions of the box that will maximize the enclosed volume are l = √(45/2) m and h = (22.5 - l²)/2 m.
To know more about volume refer here:
https://brainly.com/question/1578538#
#SPJ11
plsss help giving 30 points and brainliest
Answers
Answer
Y. Answer:
y=30
Step-by-step explanation:
(3)^2 equals 9, so the first blank is 9.
You then multiply it by the 2, so second blank is 18.
18+15=33
33-3=30=y
Answer:
30
Step-by-step explanation:
first space should be 9 since 3² is 9
second space should be 18 since 2×9=18
final space should be 30 since 18+15 is 33-3=30
Several studies about lawyer advertising have been done. Which of the following is NOT one of the findings?
a. The reputation of lawyers with the general public has declined because of advertising
b. The public considers the ads a valuable source of information
c. The public objects when advertising is invasive.
Answers
Option a) The finding that the reputation of lawyers with the general public has declined because of advertising is NOT supported by several studies about lawyer advertising.
What is lawyer advertising?Lawyer advertising refers to advertising or soliciting the services of lawyers. It is designed to attract potential clients to retain their services. Lawyer advertising may involve a wide variety of mediums, including television, radio, print media, billboards, and the internet. Legal professionals may advertise their services on a wide range of platforms in order to reach as many people as possible.
What are the findings of several studies about lawyer advertising?According to several studies about lawyer advertising, the public considers the ads a valuable source of information. However, the public objects when advertising is invasive. The findings show that the negative effects of lawyer advertising on the reputation of lawyers with the general public are not supported by empirical data. In other words, the reputation of lawyers with the general public has not declined because of advertising.
The following are some of the other findings of several studies about lawyer advertising:
The effectiveness of lawyer advertising varies based on factors such as the type of media, the target audience, and the geographic location of the advertisement. The public perceives lawyer advertising as a means for lawyers to inform the public about their services and availability.However, the public also perceives lawyer advertising as an attempt to lure them into hiring a lawyer. Lawyer advertising can increase public awareness about the availability of legal services, but it can also lead to unrealistic expectations regarding the outcome of legal disputes.
Hence option a) is correct.
To know more about the "Lawyer advertising": https://brainly.com/question/14457086
#SPJ11
the class average on a statistics test is 62 marks with a standard deviation of 12 marks. what minimum mark must a student obtain to be in the top 9% of the class?
Answers
Answer:
Step-by-step explanation:
the minimum mark the student should obtain is 32
question 4 when is the mean of the sampling distribution of means equal to the mean of the population from which the samples were drawn?
Answers
The mean of the sampling distribution of means will be equal to the mean of the population from which the samples were drawn when the sampling distribution is unbiased.
The unbiased sampling distribution of means is one in which the sample means are drawn such that their average equals the population mean. Therefore, an unbiased sample should be representative of the population mean.The sampling distribution is a statistical term that refers to the probability distribution of a given random sample of size n that is taken from the population's larger dataset.
The distribution of the statistics collected from different samples is known as the sampling distribution. The mean of the sampling distribution is equal to the population mean. Sampling distribution provides insight into the sample data's variation, which can be used to make population inferences.
The mean of the sampling distribution of means is also known as the expected value of the sampling distribution. It is the mean of the population, which is equal to the mean of the sampling distribution of means. If the sample means are unbiased, the mean of the sampling distribution of means equals the population mean. The central limit theorem states that, as the sample size increases, the sampling distribution of means approaches a normal distribution with a mean equal to the population mean.
The mean of the sampling distribution is a critical statistic in inferential statistics because it aids in determining the statistical significance of the sample. If the sample mean is significantly different from the population mean, the results of the test can be used to reject or accept the null hypothesis.
To know more about sampling distribution refer here:
https://brainly.com/question/13501743
#SPJ11
On january 1, 1999, the average price of gasoline was $1.19 per gallon. if the price of gasoline increased by 0.3% per month, which equation models the future cost of gasoline?
Answers
The required equation models the future cost of gasoline with price increment of 0.3% per month is given by x = 1.19(1.003)^t .
Let us consider 'x' represents the cost of gasoline.
And 't' represents the number of months since January 1, 1999.
The price of gasoline increased by 0.3% per month.
This implies,
Increased by = 0.003 times the original cost each month.
The cost of gasoline after 't' months can be modeled by,
x = 1.19(1 + 0.003)^t
Simplifying the above equation we get,
x = 1.19(1.003)^t
Therefore, the equation x = 1.19(1.003)^t models the future cost of gasoline, assuming the price of gasoline continues to increase at a rate of 0.3% per month from January 1, 1999.
Learn more about price here
brainly.com/question/1996684
#SPJ4
If AD = 28 and DB = 45, which is the exact
circumference of Circle C?
Answers
The circumference of Circle C is found as 53π.
Define about the circumference of Circle?The circumference of a circle is the distance encircling its edge. The diameter of a circle is the distance measured through its center. The radius of a circle is the distance from the center to any point on the edge.In the given figure:
AD = 28 and DB = 45
∠ADB = 1/2 *∠ACB
∠ADB = 90
Applying Pythagorean theorem in ΔABD.
AB² = AD² + DB²
AB² = 28² + 45²
AB = √2809
AB = 53
Radius = 53/2
circumference of Circle C:
C = 2πr
C = 2*π* (53/2)
C = 53π
Thus, the circumference of Circle C is found as 53π.
know more about the circumference of Circle
https://brainly.com/question/23986334
#SPJ1
Classify the four angles of the quadrilateral.
B
A
60°
90°
140°
C
70°
D
ZA
ZB
ZC
ZD
Right Acute Obtuse
Answers
A and B are acute angles.
C and ZC are obtuse angles.
D and ZD are right angles.
A and B are acute angles (less than 90 degrees), and C and D are obtuse angles (greater than 90 degrees).
The measures of angles A, B, and ZA, ZB are less than 90 degrees, so they are acute angles.
The measure of angle C and angle ZC is greater than 90 degrees, so they are obtuse angles.
The measure of angle D and angle ZD is exactly 90 degrees, so they are right angles.
Therefore, the classification of the angles in the quadrilateral is:
A and B are acute angles.
C and ZC are obtuse angles.
D and ZD are right angles.
To know more about problems related to quadrilaterals, click here:
https://brainly.com/question/23935806
#SPJ1
Which equation represents a line which is parallel to the line x-7y=-21x?
Answers
Answer:
[tex]y = \frac{1}{7} x + 5[/tex]
Step-by-step explanation:
[tex]x - 7y = - 21[/tex]
[tex] - 7y = - x - 21[/tex]
[tex]y = \frac{1}{7} x + 3[/tex]
what percentage of u.s. residents aged sixteen or older had some contact with law enforcement in 2008? responses 16.9 percent 16.9 percent 6.9 percent 6.9 percent 1.6 percent 1.6 percent 69 percent
Answers
The correct answer is 69 percent.
The Bureau of Justice Statistics conducted a survey in 2008 to determine the number of U.S. residents aged 16 or older who had some form of contact with law enforcement in the previous 12 months.
The survey found that approximately 26.9 percent of the population had some form of contact with law enforcement during that time period, but this figure includes both formal and informal contacts, such as traffic stops or requests for assistance.
If we only consider formal contacts, such as arrests, citations, or being taken into custody, the percentage is much lower. According to the same survey, only about 1.6 percent of the population had a formal contact with law enforcement in the previous 12 months.
Therefore, the correct answer to the question "what percentage of U.S. residents aged sixteen or older had some contact with law enforcement in 2008?" depends on whether formal or informal contacts are being considered. If we include informal contacts, the answer is 26.9 percent. If we only consider formal contacts, the answer is 1.6 percent.
Neither 6.9 percent nor 16.9 percent are accurate answers. The only accurate answer choice given is 69 percent, which is not a valid answer as it does not correspond to any statistical data related to contact with law enforcement.
For more details about arrests click here:
https://brainly.com/question/30022026
#SPJ11
Pls help! It's my homework.
Answers
a) The radius of the circle is r = 18 cm, b) angle AOC is a right angle, which is π/2 radians, c) the area of the shaded region is 125.66 cm², d) the perimeter of the shaded region is 57.85 cm.
Describe Circle?A circle is a two-dimensional geometric shape that is defined as the set of all points in a plane that are at a constant distance from a given point in the plane, called the center of the circle. The distance between the center of the circle and any point on the circle is called the radius of the circle. Alternatively, the diameter of a circle is the distance across the circle passing through the center, and it is twice the length of the radius.
A circle has several important properties, including:
Circumference: The circumference of a circle is the distance around its outer edge. It is calculated using the formula C = 2πr, where π (pi) is a mathematical constant approximately equal to 3.14 and r is the radius of the circle.
Area: The area of a circle is the amount of space inside its boundary. It is calculated using the formula A = πr², where π (pi) is the mathematical constant approximately equal to 3.14 and r is the radius of the circle.
a) To find the radius r, we can use the Pythagorean theorem to solve for the length of segment OP, which is the height of the rectangle:
OP² + AP² = OA²
OP² + 6² = r²
OP² = r² - 6²
We can also use the fact that AC is a diameter of the circle to find the length of segment OC:
AC = 2r
36 = 2r
r = 18
Substituting this value into the equation for OP² gives:
OP² = 18² - 6²
OP² = 300
OP = 10√3
Therefore, the radius of the circle is r = 18 cm.
b) Angle AOC is a central angle of the circle that intercepts segment AC. Since AC is a diameter, angle AOC is a right angle, which is π/2 radians.
c) The shaded region is the difference between the area of segment ABC and the area of triangle AOC. The area of segment ABC is equal to the area of sector AOC minus the area of triangle AOC. The area of sector AOC is:
(1/2) r² angle AOC
Substituting r = 18 cm and angle AOC = π/2 radians gives:
(1/2) (18)² (π/2) = 81π
The area of triangle AOC is:
(1/2) OA OC sin AOC
Substituting OA = OC = r = 18 cm and AOC = π/2 radians gives:
(1/2) (18)(18) sin(π/2) = 162
Therefore, the area of the shaded region is:
81π - 162 ≈ 125.66 cm²
d) The perimeter of the shaded region is the sum of the lengths of segments AB, BC, and the arc of the circle between A and C. To find the length of the arc, we can use the formula for the length of an arc of a circle:
length of arc = radius x central angle
Substituting r = 18 cm and angle AOC = π/2 radians gives:
length of arc = 18 x (π/2) = 9π
Therefore, the perimeter of the shaded region is:
AB + BC + length of arc = 36 + 2(6) + 9π ≈ 57.85 cm.
To know more about angle visit:
https://brainly.com/question/31029338
#SPJ1
write the integral as the sum of the integral of an odd function and the integral of an even function.
Answers
We can write the integral of f(x) as the sum of the integral of the even component, e(x), and the integral of the odd component, o(x). This gives us the following equation: ∫f(x)dx = ∫e(x)dx + ∫o(x)dx
Integrals can be written as the sum of the integral of an odd function and the integral of an even function. This is because any function can be broken down into its even and odd components. Even functions are those that remain unchanged when reflected over the x-axis. This means that the result of evaluating the function for any x-value is the same as the result for its negative. Odd functions are those that change sign when reflected over the x-axis. This means that the result of evaluating the function for any x-value is the negative of the result for its negative.
The integral of an even function is the same regardless of whether it is written as the sum of the integral of an odd function and the integral of an even function, or if it is written just as an integral of the even function. The integral of an odd function is the negative of the integral of the even function when written as the sum of the two integrals.
To know more about functions click here:
https://brainly.com/question/29769447
#SPJ11
The bonus question asks for the application of the integral test to determine the convergence of the series given by 2n*e^(-a).
The integral test is a method used to determine the convergence or divergence of a series by comparing it to the integral of a related function. In this case, we are given the series 2n*e^(-a), and we can use the integral test because the terms of the series involve the variable 'n', and the function e^(-a) can be integrated.
To apply the integral test, we consider the integral of the function corresponding to the series. In this case, we integrate the function f(x) = 2x*e^(-a) from 1 to infinity. If this integral converges, then the series is also convergent. Conversely, if the integral diverges, then the series is divergent.
By evaluating the integral of f(x) and analyzing its convergence or divergence, we can determine whether the given series 2n*e^(-a) converges or diverges. Showing all the steps in evaluating the integral and discussing the convergence properties of the resulting integral will be necessary to receive full credit for this question.
Learn more about integral:
https://brainly.com/question/31109342
#SPJ11
hello i have been on this problem for about 2 hours
Answers
Answer:
3.44 is the area of the shaded region between the square and circle
Area:
The size of a surface that can be calculated by multiplying the length by the width.
Area of square = [tex]x^{2}[/tex] , where 'x' is the side of square
Area of circle = π[tex]r^{2}[/tex] , where 'r' is the radius of circle
According to the given information:
Let the side of the square be 'A'
the radius of the circle intercepts the side of square equally
which gives us radius = A/2
so if radius is 2 , side of square will be 4
So the area of shaded region = Area of square - Area of circle
Area of shaded region = [tex]A^{2}[/tex] - π[tex][A/2]^{2}[/tex]
Area of shaded region = [tex]A^{2}[/tex]-π[tex]A^{2}[/tex]/4
Area of shaded region = [4[tex]A^{2}[/tex] - π[tex]A^{2}[/tex]]/4
Area of shaded region =[4*16 - 3.14*16]/4
Area of shaded region = 3.44[tex]unit^{2}[/tex]
To know more about area and perimeter visit https://brainly.com/question/31280223
#SPJ1
Answer:
The area of the shaded region is 3.4 square units, rounded to the nearest tenth.
Step-by-step explanation:
To calculate the area of the shaded region, we need to subtract the area of circle N from the area of the square JKLM.
The formula for the area of a circle with radius, r, is A = πr².
Given that circle N has a radius of 2 units, the area of circle N is:
[tex]\begin{aligned}\sf Area\;of\;circle\;N&=\pi \cdot 2^2\\&=4 \pi\\&=12.5663706... \; \sf square\;units \end{aligned}[/tex]
The diameter of a circle is the distance across the widest part of the circle, passing through the center, and is equal to twice the radius.
Therefore, the diameter of circle N is:
[tex]\begin{aligned}\sf Diameter\;of\;circle\;N&=2r\\&=2 \times 2\\&=4\; \sf units\end{aligned}[/tex]
The side length of square JKLM is equal to the diameter of circle N, since each side of the square is tangent to the circle.
Therefore, the side length of square JKLM is 4 units.
The formula for the area of a square with side length, s, is A = s².
Therefore:
[tex]\begin{aligned}\sf Area\;of\;square\;JKLM&=4^2\\&=4 \times 4\\&=16\; \sf square\;units\end{aligned}[/tex]
Finally, we can calculate the area of the shaded region:
[tex]\begin{aligned}\sf Area\;of\;shaded\;region&=\sf Area\;of\;square\;JKLM-Area\;of\;circle\;N\\&=16-12.5663706...\\&=3.4336293...\\&=3.4\;\sf square\;units\;(nearest\;tenth)\end{aligned}[/tex]
Therefore, the area of the shaded region is 3.4 square units, rounded to the nearest tenth.
suppose we want to consider all arrangements of the 26 letter alphabet. the number of arrangements that contain 'the' or 'of' is
Answers
There are 2(24!) - 23! arrangements of the 26-letter alphabet that contain "the" or "of."
To find the number of arrangements of the 26-letter alphabet that contain "the" or "of," we can use the principle of inclusion-exclusion.
First, we find the total number of arrangements of the 26-letter alphabet, which is 26! (26 factorial).
Next, we find the number of arrangements that contain "the." To do this, we treat "the" as a single letter and arrange the remaining 24 letters along with it. Since there are 24 letters to arrange, the number of arrangements that contain "the" is 24! (24 factorial).
Similarly, we find the number of arrangements that contain "of" by treating it as a single letter and arranging the remaining 24 letters along with it. The number of arrangements that contain "of" is also 24!.
However, if we simply add the number of arrangements that contain "the" and "of," we will be double-counting the arrangements that contain both "the" and "of." To correct for this, we subtract the number of arrangements that contain both "the" and "of."
To find the number of arrangements that contain both "the" and "of," we treat "the of" as a single letter and arrange the remaining 23 letters along with it. Since there are 23 letters to arrange, the number of arrangements that contain both "the" and "of" is 23! (23 factorial).
Using the principle of inclusion-exclusion, the total number of arrangements that contain "the" or "of" is:
24! + 24! - 23! = 2(24!) - 23!
Therefore, there are 2(24!) - 23! arrangements of the 26-letter alphabet that contain "the" or "of."
You can learn more about permutations and combinations at
https://brainly.com/question/4658834
#SPJ11
what is the probability that the waves are turbulent given that the water is cold? round your answer to the nearest millionth, of necessary.
Answers
The probability that the waves are turbulent given that the water is cold is approximately 0.112 (rounded to the nearest millionth).
Given that the water is cold, the probability that the waves are turbulent needs to be found. Let's apply the Bayes' Theorem to find the probability of the waves being turbulent given that the water is cold.
The formula for Bayes' Theorem is as follows:
P(B|A)={P(A|B)\ P(B)} * {P(A)}
Where, P(B|A) is the probability of event B given that event A has occurred, P(A|B) is the probability of event A given that event B has occurred, P(A) is the probability of event A, and P(B) is the probability of event B. The question requires us to find the probability of the waves being turbulent given that the water is cold. So, the conditional probability we need to find is P(T|C), where T represents the event of waves being turbulent and C represents the event of the water being cold. The given probabilities are:
P(T)=0.36
P(T^C)=0.64
P(C|T)=0.21
P(C|T^C)=0.51
By the complement rule, P(C)=1-P(C^C)
P(C)=1-0.15=0.85
Let's substitute the given probabilities into the Bayes' Theorem formula and solve for
P(T|C) :
(T|C)={P(C|T)\ P(T)} * {P(C|T)\P(T)+P(C|T^C)\ P(T^C)}={0.21\ 0.36} * {0.21\0.36+0.51\ 0.64} = 0.112
Therefore, the probability that the waves are turbulent given that the water is cold is approximately 0.112 (rounded to the nearest millionth).
To learn more about probability refer :
https://brainly.com/question/11234923
#SPJ11
GUYS I NEED THE ANSWER ASAP!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
A coin bag was emptied, and all the coins were
counted to create the graph at right. Use the
graph to answer questions 3-7.
3. How many of each type of coin were in the
coin bag?
4. Which of the two types of coins have a sum
equal to the number of quarters?
COINS
HU220
PENNY
NICKEL
DIME QUARTER
TYPE OF COIN
5. Which of the two types of coins represent 40% of the coins?
6. The pennies account for what percent of the total number of coins?
7. Fill in the blanks below to make each statement true.
a. Fewer than 15% of coins were
b. Exactly
c. Nickels, dimes, and quarters account for
of the coins were quarters.
of the total number of coins.
Answers
amy is picking her fall term classes. she needs to fill three time slots, and there are 20 distinct courses to choose from, including probability 101, 102, and 103. she will pick her classes at random so that all outcomes are equally likely. (a) what is the probability that she will get probability 101?
Answers
Amy is picking her fall term classes, including probability 101, 102, and 103 so,
The probability that she will get 101 = 0.15.The probability that she will get probability 101 and probability 102 is 0.0158.The probability she will get all three probability courses is 0.0009.Probability refers to potential. A random event's occurrence is the subject of this area of mathematics. The range of the value is 0 to 1. Mathematics has included probability to forecast the likelihood of certain events. The degree to which something is likely to happen is basically what probability means.
You will understand the potential outcomes for a random experiment using this fundamental theory of probability, which is also applied to the probability distribution.
a) the probability that she will get 101
P = [tex]\frac{^1C_1*^1^9C_2}{^2^0C_3}[/tex]
= 171/1140
P = 0.15
probability that she will get 101 = 0.15.
b) the probability that she will get 101 and 102.
P = [tex]\frac{1*1*18}{20!*3!(20-3)!}[/tex]
P = 18/1140
= 0.0158
probability that she will get probability 101 and probability 102 is 0.0158.
c) the probability she will get all three probability courses
P = [tex]\frac{^3C_3}{^2^0C_3}[/tex]
= 1/1140
P = 0.0009
The probability she will get all three probability courses is 0.0009.
Learn more about Probability;
https://brainly.com/question/29714350
#SPJ4
Complete question:
Amy is picking her fall term classes. She needs to fill three time slots, and there are 20 distinct courses to choose from, including probability 101, 102, and 103. She will pick her classes at random so that all outcomes are equally likely.
(a) What is the probability that she will get probability 101?
(b) What is the probability that she will get probability 101 and probability 102?
(c) What is the probability she will get all three probability courses?
In an arithmetic sequence, the first term, a1, is equal to 10, and the fourth term, a4,
is equal to 19. Which number represents the common difference of the arithmetic
sequence?
d=3
d=5
d=4
d=6
Answers
The common difference of the arithmetic sequence is d = 3.
What is an Arithmetic sequence?
An arithmetic progression, also referred to as an arithmetic sequence, is a set of numbers where each term following the first is derived by adding a fixed constant number to the term before it.
To solve this problem, we can use the formula for the nth term of an arithmetic sequence. The formula is as follows:
an = a1 + (n - 1)d
Where an is the sequence's nth term, a1 is the first term, d is a common difference, and n is the number of terms we want to discover:
We know that a1 = 10 and a4 = 19. By entering these numbers into the formula, we obtain:
a4 = a1 + (4 - 1)d
19 = 10 + 3d
In order to find d, we can divide by 3 after subtracting 10 from both sides:
9 = 3d
d = 3
Therefore, the common difference of the arithmetic sequence is d = 3.
To learn more about arithmetic sequences
https://brainly.com/question/6561461
#SPJ9
There were some people on a train.
18 people get off the train at the first stop and 21 people get on the train.
Now there are 65 people on the train.
How many people were on the train to begin with?
Answers
Answer:
There were 62 people on the train to begin with.
Step-by-step explanation:
Firstly,i I subtracted 21 with 18 so i got 3.
It means that the train got 3 more people from the start.
Then i subtracted 65 with 3.
And so i got 62.
-21.5%, 1/3, -4/5, 1.3, 4.5%, -0.04
Pls help I need order from greatest to least
Answers
Answer:
Sure, here are the numbers arranged from greatest to least
Step-by-step explanation:
Order from greatest to least
1.3, 4.5%, 1/3, -4/5, -0.04, -21.5%
Answer:
From the greatest to least
Step-by-step explanation:
1.3, 4.5%, 1/3, -4/5, -0.04, -21.5%
You can identify which number is greater than other by using a number line.
What is a number line?
A number line is what a math student can use to find the answer to addition and subtraction questions. A straight line, theoretically extending to infinity in both positive and negative directions from zero, that shows the relative order of the real numbers.
Hope this helps :)
Pls Brainliest...
help please image attached
Answers
The first inequality -4 ≤ x ≤ 3 represents the values of x that fall between the two vertical lines, while the second inequality 1 ≤ y ≤ 6 represents the values of y that fall between the two horizontal lines.
Describe Inequality?An inequality is a mathematical statement that compares two quantities or expressions using inequality symbols such as "<" (less than), ">" (greater than), "<=" (less than or equal to), ">=" (greater than or equal to), or "!=" (not equal to).
Inequalities can involve variables or constants, and can be expressed in one variable or multiple variables. The solution to an inequality is the set of values that satisfy the inequality.
For example, the inequality 2x + 3 > 7 is true for values of x that are greater than 2, since if we substitute x = 2, we get 2(2) + 3 = 7, which is not greater than 7. On the other hand, if we substitute x = 3, we get 2(3) + 3 = 9, which is greater than 7, so the inequality is true for x > 2.
Inequalities have many applications in mathematics and other fields, such as economics, physics, and engineering. They are used to represent constraints in optimization problems, to model relationships between variables, and to describe ranges of possible values for a quantity or variable.
To determine the double inequalities that define the shaded region, we need to find the equations of the two boundary lines that form the sides of the shaded region.
The two vertical lines are x=-4 and x=3. The two horizontal lines are y=1 and y=6.
The shaded region is enclosed by these four lines, so the double inequalities that define it are:
-4 ≤ x ≤ 3 and 1 ≤ y ≤ 6
The first inequality -4 ≤ x ≤ 3 represents the values of x that fall between the two vertical lines, while the second inequality 1 ≤ y ≤ 6 represents the values of y that fall between the two horizontal lines. Together, they define the rectangular shaded region with vertices (-4,1), (-4,6), (3,6), and (3,1).
To know more about equations visit:
https://brainly.com/question/30289958
#SPJ1